Le nombre Pi

Le nombre p

Qu'est-ce que le nombre p ?

Le nombre p et son histoire

Des décimales de p

Fraction continue

Valeurs approchées de p

Quelques belles formules

Des poèmes pour retenir Pi

Des programmes de calcul de p en javascript

D'autres petites choses marrantes ...

Calculer p avec des élèves

Quelques liens

Qu'est-ce que le nombre p ?
"p = 3,14" comme on dit ... Mais qu'est-ce que ce nombre p ( pi ) au juste ?

Pour le commun des mortels ...
Tout le monde (enfin, ... en principe !) connaît la formule qui donne le périmètre d'un cercle à partir de son diamètre ou de son rayon et du nombre p qui vaut quelque chose comme 3,1415926535... :

soit

que l'on écrit

D'où la définition classique de pi qui est :

p ( pi ) est le rapport constant entre la longueur d'un cercle (le périmètre du cercle) et son diamètre (le double de son rayon).

ou encore

Ou bien encore, à partir de la formule permettant de calculer l'aire (la "surface") d'un disque (le disque est la surface comprise à l'intérieur du cercle) à partir de son rayon :

soit

on obtient la définition suivante de pi (qui est équivalente à la précédente) :

p ( pi ) est le rapport constant entre l'aire d'un disque et le carré de son rayon.

Pour le mathématicien ...
La définition n'est pas la même.
La définition donnée précédemment à l'aide du périmètre du cercle ou de l'aire du disque est ennuyeuse pour le mathématicien car elle suppose que l'espace dans lequel on se place soit euclidien pour que le rapport "périmètre du cercle / diamètre" soit constant et indépendant du cercle choisi (ce qui n'est pas vrai lorsqu'on trace des cercles sur une sphère, par exemple) et également qu'une théorie de l'intégration soit développée sur cet espace pour pouvoir calculer le périmètre du cercle ou l'aire du disque.

Aussi les mathématiciens préfèrent-ils une définition basée sur l'analyse.
Evidemment, elle est équivalente à la définition précédente. On obtient toujours le même nombre pi !

Voici la définition que l'on peut trouver dans un livre d'analyse (Analyse, J.-M. Arnaudiès et H. Fraysse, Editions Dunod, 1988, page 217)

On appelle pi et on note p le double de l'unique racine de l'équation cos(x) = 0, comprise entre 0 et 2.
( La fonction cos ayant été définie à la page 210 par

)

Ce qui est équivalent à :

p ( pi ) est le plus petit nombre réel a > 0 tel que cos(a) = -1

Ou bien encore,

p ( pi ) est la moitié de la période fondamentale de la fonction cosinus, c'est-à-dire :
p est le plus petit nombre réel a > 0 tel que

cos étant la fonction cosinus définie à partir de la fonction exponentielle, elle-même définie comme la somme d'une série entière sur l'ensemble des nombres complexes...

Pour tout nombre complexe z,

soit

Démonstration
Pour de plus amples détails et des démonstrations sur cette définition (définition par série entière, convergence, dérivabilité, périodicité, ...etc des fonctions réelles et complexes exponentielles, cosinus et sinus, équivalence avec la définition classique de pi), télécharger le document suivant :

Définition par série entière des fonctions réelles et complexes exponentielles, cosinus et sinus :
fichier PDF non zippé, 325 ko	fichier PDF zippé, 42 ko

Pour Bourbaki ...
Nicolas Bourbaki est le nom d'un collectif de mathématiciens qui ont entrepris depuis 1935 de réécrire l'ensemble des mathématiques de la manière la plus rigoureuse possible, dans un ensemble d'ouvrages nommé Eléments de mathématiques.
Dans le volume Fonctions de variable réelle ( FVR), Bourbaki défini le nombre pi.
Pour cela, il a été défini dans le volume de Topologie générale (TG, VII, p.8) l'homomorphisme continu x |--> e(x) du groupe additif (R, +) sur le groupe multiplicatif (U, .) des nombres complexes de module 1, fonction périodique de période 1 et telle que e(1/4) = i.
Pourquoi faire simple quand on peut faire compliqué ?
En réalité, nous connaissons tous cette fonction sous le nom de x |--> exp(2ipx) ...

Ensuite, en FVR II.4, arrive la proposition 3 :

La fonction e(x) admet en tout point de R, une dérivée égale à 2pi e(x), où p est une constante >0.

Dans la démonstration de cette proposition, il est démontré que la dérivée de le fonction e(x) est égale à a e(x) où a est une constante et a >0.
Ensuite, il est dit : "il est d'usage de désigner le nombre a ainsi défini par la notation 2p."

Et voila comment Bourbaki nous montre que le voyage en haute altitude que nous croyions effectuer n'était en fait qu'une promenade au milieu d'un paysage qui nous est très familier mais qui était juste un peu ... embrumé !
"Il est d'usage" ...

Pour la Bible ...
Dans le passage de la Bible 1. Rois 7.23 :

"Il fit la Mer en métal fondu, de dix coudées de bord à bord, à pourtour circulaire de 5 coudées de hauteur ; un fil de 30 coudées en mesurait le tour"

Ceci donne la valeur 3 pour p.
Dieu n'aurait-il pas arrêté son calcul un peu trop vite ?
Ou bien l'univers que Dieu a créé n'est pas euclidien et a une courbure telle qu'un cercle a pour circonférence le triple de son diamètre ? ...

Retour vers le haut de la page

Le nombre p et son histoire

L'historique de p

Les premiers calculs de décimales du nombre p

La notation " p "

Nature algébrique de p

La quadrature du cercle

Nombres constructibles à la règle et au compas

Retour vers le haut de la page

L'historique de p

Le nombre pi est connu depuis l'antiquité, évidemment, pas au sens où nous l'entendons maintenant (notion abstraite de constante mathématique) mais en tant que rapport entre la longueur du cercle et son diamètre et d'ailleurs surtout en tant que méthode de calcul du périmètre du cercle (ou de l'aire du disque).
Les notations utilisées sont les notations actuelles (signes + et = , trait de fraction , notation décimale), qui sont utilisées depuis le XVIème siècle.

En 2000 av.JC, les Babyloniens connaissaient Pi (comme le rapport constant entre la circonférence d'un cercle et son diamètre, mais pas comme objet mathématique).
Ils avaient comme valeur 3 + 7/60 + 30/3600 (ils comptaient en base 60) soit 3 + 1/8 = 3,125.

Vers 1650 av.JC, les Egyptiens avaient comme valeur (16/9)² qui vaut environ 3,16. Cette valeur a été retrouvée sur le fameux papyrus de Rhind, écrit par le scribe Ahmès, acheté par un Ecossais qui s'appelle ... Henry Rhind. Il est conservé au British museum.

Le Papyrus de Rhind provient du temple mortuaire de Ramsès II à Thèbes, en Egypte (la ville où est érigé le temple de Karnak) et fut acheté par Alexander Rhind.
Il a été écrit vers -1650 par le scribe Ahmès. Constitué de 14 feuilles de papyrus, il mesurait à l'origine plus de 5 m de longueur sur 32 cm de large. Il est le plus vieux traité de mathématiques du monde et contient 87 problèmes dont, par exemple, la décomposition des fractions en fractions unitaires (dont le numérateur est 1), de l'arithmétique ( multiplications et divisions ), résolution d'équations, l'arpentage (mesures des distances) et à la géométrie : aires planes (du trapèze en particulier), volumes de greniers à grains, calcul de pyramides .

Cliquez sur l'image
pour la voir en plus grand

Ensuite, pi apparaît :

En Chine vers 1200 av.JC, avec pour valeur 3.
Dans la Bible vers 550 av.JC, avec pour valeur 3.
En Grèce , avec en particulier Archimède en 250 av.JC qui donne l'encadrement 223/71 < pi < 22/7 et Ptolémée en 150 qui utilise 3 +8/60 + 30/3600 = 3,1416666.
En Chine au Vème siècle , avec pour valeur 355/113.
En Inde : 3 + 177/1250 = 3,1416 en 380 puis 3,16227 (racine carrée de 10) avec Brahmagupta en 640
Au Moyen-Orient avec Al Khwarizmi en 800 (Ouzbekistan) et Al Kashi en 1429 (Turkestan) qui calcule 14 décimales de pi.
En Europe : l'Italien Fibonacci, en 1220, trouve la valeur 3,141818, au Pays-Bas avec Van Ceulen (20 décimales en 1596 puis 34 décimales en 1609 !), en France avec Viète (9 décimales en 1593).

Ensuite vint le développement des techniques de calculs avec l'analyse (dérivée, intégrales, sommes de séries, produits infinis ...), Wallis en 1655, Newton (16 décimales en 1665), Gregory, Leibniz, Machin (100 décimales en 1706), puis Euler (20 décimales calculées en une heure ! )vers 1760 et beaucoup d'autres.

Les champions contemporains sont les frères Chudnovsky avec 4 milliards de décimales en 1994 et Kanada et Tamura dont le dernier record datait de 1999 avec 206 milliards de décimales (en environ 33 heures de calculs).
Kanada a battu son propre record le 6 décembre 2002 avec une équipe de neuf autres chercheurs japonais du Information Technology Centre de l'Université de Tokyo : 1 241 100 000 000 décimales ont été calculées à l'aide d'un super calculateur Hitachi (400 heures de calculs !) en utilisant un algorithme que l'équipe a mis cinq ans à mettre au point.

Retour au menu "le nombre p et son histoire"

Les premiers calculs de décimales du nombre pi

C'est Archimède (né en 287 av. JC à Syracuse et mort en 212 av. JC) , en 250 av.JC qui a réellement commencé à calculer des décimales du nombre pi. Il est surtout le premier à avoir utilisé un algorithme pour le calcul.
La méthode, qu'on appelle naturellement aujourd'hui la méthode d'Archimède, consiste à calculer le périmètre de polygones réguliers inscrits et circonscrits au cercle pour encadrer le périmètre du cercle et donc en déduire un encadrement de pi. Il obtint ainsi

3+10/71 < p < 3+1/7

Quelques détails sur l'algorithme d'Archimède

Retour au menu "le nombre p et son histoire"

La notation p
p est la première lettre du mot grec perimetron, périmètre ou perijereia, circonférence, périphérie.

Il y a plusieurs versions sur l'apparition du symbole, mais l'époque est toujours la même : vers 1600.
William Oughtred (1574-1660) en 1647 et Isaac Barrow (1630-1677) utilisent le symbole p pour représenter le périmètre d'un cercle de diamètre 1.
Un Allemand, Ludolph von Ceulen (1539-1610) utilisait déjà cette notation.
Qui fut le premier ? Est-ce bien important ? Il serait néanmoins intéressant de savoir si ces personnes communiquaient et comment l'usage du symbole p s'est répandu.

En 1706 , Jones l’utilise pour désigner le rapport de la circonférence d’un cercle à son diamètre (à cette époque , Bernoulli emploie la lettre c)

Euler , utilise la lettre p ,dans un ouvrage sur les séries, publié en latin en 1737 puis, en 1748, dans son ’’Introduction à l’analyse infinitésimale’’, ce qui imposa définitivement cette notation .

Retour au menu "le nombre p et son histoire"

Nature algébrique de p
p n'est pas un nombre décimal, c'est-à-dire que les chiffres après la virgule ne sont pas en nombre fini (p a une infinité de décimales).
La meilleure valeur décimale approchée de p connue actuellement comporte environ 1241 milliards de chiffres ... Autant dire presque rien !

p est un nombre irrationnel, c'est-à-dire qu'il ne peut pas s'écrire comme une fraction de deux nombres entiers. Autrement dit, cela signifie aussi que les chiffres de p ne sont pas prévisibles. On ne peut pas deviner une décimale sans la calculer explicitement, comme qu'on peut le faire avec le nombre 1/7 = 0,14285714285714... par exemple.
L'irrationnalité de p fut démontré en 1761 par l'Allemand Lambert.

p est un nombre transcendant c'est-à-dire qu'il n'est solution d'aucune équation à coefficients rationnels. Cela fut démontré en 1881 par Lindemann.

Retour au menu "le nombre p et son histoire"

La quadrature du cercle
La quadrature du cercle est un des grands problèmes de géométrie de l'antiquité et l'est resté pendant longtemps.
Il consiste à construire à la règle et au compas un carré de même aire qu'un disque de rayon donné, ce qui revient à construire le nombre (plus exactement le rapport) égal à la racine carrée de p. Il fallut attendre 1882 pour que Lindemann démontre que p est un nombre transcendant (i.e solution d'aucune équation à coefficients rationnels), ce qui prouve que p n'est pas constructible à la règle et au compas.

Retour au menu "le nombre p et son histoire"

Nombres constructibles à la règle et au compas (petit complément pour les curieux...)

Un nombre x est dit constructible à la règle et au compas si le point de coordonnées (x,0) peut être obtenu par une suite finie d'intersections de droites et de cercles construits à partir des deux points de coordonnées (0,0) et (1,0).

On a le théorème suivant (voir Cours d'algèbre, Daniel Perrin)

si un nombre réel x est constructible à la règle et au compas, alors le degré de l'extension de corps Q[x] sur Q est une puissance de 2.

Or p est transcendant donc le degré de Q[p] sur Q est infini . Donc p n'est pas constructible.

Deux petites remarques , tant qu'on y est !
Ce même théorème balaie également les deux autres problèmes grecs : la duplication du cube et la trisection de l'angle.

La duplication du cube revient à construire à la règle et au compas un nombre a tel que le cube d'arête a ait un volume double du cube unité. Autrement dit a³=2 c'est-à-dire que a est la racine cubique de 2.
Mais le polynôme X³-2 est irréductible sur Q et c'est donc le polynôme minimal de a. Donc le dégré de Q[a] sur Q est 3, qui n'est pas une puissance de 2.
La trisection de l'angle est le problème qui consiste à partager un angle donné en trois angles égaux à la règle et au compas. Ce problème revient à construire le nombre cos(t) connaissant le nombre cos(3t) .
La formule cos(3t) = 4 cos³(t) - 3 cos(t) montre que x = cos(t) est racine du polynôme 8X³ -6X -1qui est irréductible sur Q. Donc le degré de Q[x] sur Q est 3, qui n'est toujours pas une puissance de 2.

Retour au menu "le nombre p et son histoire"

Retour vers le haut de la page

Des décimales du nombre p
Depuis le 31 décembre 2009, il est connu environ 2 700 000 000 000 (environ 2700 milliards !) de décimales du nombre pi ...
Pour en savoir plus : http://bellard.org/pi/pi2700e9/

Ä quoi cela sert-il de connaître tant de décimales de pi ?

Le calcul de décimales de pi est un très bon test pour vérifier la précision des calculs des ordinateurs (deux erreurs graves furent ainsi détectées sur les super-ordinateurs IBM 590 et R8000)
La recherche de "motifs" de régularité et les calculs de statistiques sur les chiffres du nombre pi nécessitent de connaître de plus en plus de décimales.
Mais la motivation la plus importante n'est pas de connaître de plus en plus de décimales de pi mais bel et bien de les calculer. En effet, le calcul d'un si grand nombre de chiffres demande des algorithmes de calculs très perfectionnés et a permis de très grand progrès dans ce domaine.

Les 100 premières décimales de pi :

3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067

Les 627 premières décimales de pi

Elles sont affichées dans la salle (circulaire) de mathématiques
du Palais de la Découverte.

Les 2400 premières décimales de pi : Cliquez ici pour les voir Cliquez ici pour les télécharger

Le programme qui calcule les 2400 premières décimales de pi : Télécharger le programme (Fichier .bas)
C'est un programme en QuickBasic (vous savez, le vieux langage Basic sous MS-Dos...). Si vous n'avez pas ou plus le programme QuickBasic.exe, je vous le redonne (Il suffit de cliquer sur le mot QuickBasic.exe).
Je prépare la conversion en Javascript... Patience.

Un million de décimales de pi : Cliquez ici pour les télécharger (Fichier .Zip, 471Ko)

Un programme de calcul de décimales de pi : PiFast32 (Fichier .Zip, 118Ko)
Ce programme est très efficace et vraiment très impressionnant : il calcule 10 000 décimales en 0,83s et 100 000 décimales en 3,85s sur un Pentium II 233Mhz !!
Une petite remarque : ce programme ne sait pas calculer moins de 10 000 décimales ...

Une frise pour afficher les décimales de pi : Cliquez ici pour les télécharger (Fichier pdf zippé : 62ko)
1000 décimales de pi à afficher dans une classe sous forme d'une bande de 27 mètres de long ...

Retour vers le haut de la page

Fraction continue

On appelle fraction continue l'écriture d'un nombre réel sous la forme : où les a_i et b_i sont des nombres entiers. La suite des nombres a_i et b_i ne s'arrête pas nécessairement.	,
Si tous les nombres b_i sont égaux à 1, la fraction continue est dite régulière : On la note alors *[a₀ , a₁ , a₂ , ... , a_i , ...]*

La fraction continue régulière de p est :

Avec l'autre notation, en voici plus de "chiffres" :
p = [ 3, 7, 15, 1, 292, 1, 1, 1, 12, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, ...]

p n'est pas un nombre rationnel mais peut-etre approché de très près par des fractions de nombres entiers.
Par exemple : 314 / 100 est une fraction de deux entiers qui donne une valeur approchée de p avec deux chiffres exacts après la virgule.
En réalité, on peut approcher p par une fraction d'entiers donnant une valeur avec autant de chiffres que l'on veut après la virgule .
Les meilleures approximations rationnelles de p sont les fractions réduites de son développement en fraction continue.
En voici deux exemples :

Voici les premières réduites de p :
3 / 1 ; 22 / 7 ; 333 / 106 ; 355 / 113 ; 103993 / 33102 ; 104348 / 33215 ; 208341 / 66317 .

Retour vers le haut de la page

Valeurs approchées de p
Voici des éclaircissements sur quelques valeurs approchées célèbres de p, qui circulent dans les repas de famille et qui génèrent immanquablement des questions aux profs de maths ...

Tout d'abord, AUCUNE des valeurs données ci-dessous n'est LA valeur du nombre p.
p n'est pas un nombre décimal donc ces chiffres après la virgule ne s'arrêtent pas.
p n'est pas un nombre rationnel donc aucune fraction de nombres entiers n'est égale à p.

"Trois quatorze" (3,14) : la plus connue. Valeur approchée de p avec deux chiffres exacts après la virgule. C'est une très bonne valeur pour la plupart des calculs.
"Trois quatorze cent seize" : celle-ci mérite une bonne explication.
Première explication possible : elle date de l'ancien temps où l'on disait "quatorze cent seize" pour lire le nombre 1416 comme on dit "quinze cent quinze" pour la bataille de Marignan.
"Trois quatorze cent seize" est donc la valeur 3,1416 qui est une valeur arrondie avec quatre chiffres après la virgule (le dernier chiffre, 6, n'est pas exact mais arrondi). Cette expression occasionne souvent la valeur fausse 3,14116 .
Deuxième explication possible : elle date également de l'ancien temps où les instituteurs faisaient apprendre la valeur 3,1416. Dans les calculs il fallait utiliser la valeur 3,14 c'est-à-dire "trois quatorze SANS seize". Cette explication m'a été fourni par Gérard Colin, merci à lui.
"Trois quatorze cent seize" est donc la valeur 3,1416 qui est une valeur arrondie avec quatre chiffres après la virgule (le dernier chiffre, 6, n'est pas exact mais arrondi). Cette expression occasionne souvent la valeur fausse 3,14116 .
"Vingt-deux septièmes" ( 22/7 ) : il y en a régulièrement qui soutiennent que c'est LE nombre p ...
En réalité, c'est la fraction la plus simple qui approche le mieux p. C'est la première fraction réduite du développement de pi en fraction continue : 3 + 1/7 = 21/7 + 1/7 = 22/7. A noter que c'est une valeur qu'Archimède avait calculée aux environs de 250 avant JC pour encadrer p. 22/7 vaut 3,142 857 142 857 142 ... et donne une valeur approchée de p avec deux chiffres exacts après la virgule.
355/113 : moins connue mais c'est une très bonne approximation rationnelle de p ( valeur approchée qui est une fraction de nombre entiers).
C'est une réduite du développement de pi en fraction continue : 3 + 1 / (7 + 1 / (15 + 1/ 1 ).
355 / 113 vaut environ 3,141 592 92 qui est une valeur de p avec 6 chiffres exacts après la virgule (3,141592).

Lorsque l'on demande à un mathématicien combien vaut p, il répond : " p ! " ...

Retour vers le haut de la page

Quelques belles formules faisant intervenir p
La formule d'Euler
La plus belle à mon avis. Elle réunit les nombres les plus importants du monde mathématique avec une telle simplicité …

ou bien encore

Quelques formules liant les entiers et pi.

	Viète (1540-1603) Ce fut la premirère formule "infinie" donnant pi
	Wallis (1616-1703 Anglais) Ce fut la première formule "infinie" donnant pi sans racines carrées
	Une autre manière de voir la formule de Wallis
	Brounker (1620-1684, anglais, premier président de la Royal Society)
	Grégory (1638-1675 Ecossais) donna le développement d'Arctan(x) en série entière et Leibniz (1646-1716 Allemand) donna cette formule en l'appliquant à x = 1
	Leibniz (1646-1716)
	Euler (1707-1783 Suisse)
	Borwein et Plouffe Formule utilisée pour calculer les chiffres de pi en base 2 (en base 10, on dit décimale, en base 2, on dit digit)

Cette dernière, dûe à Euler, est la formule qui est utilisée par le programme calculant les 2400 décimales de Pi.

Une formule qui relie pi et le nombre d'or

étant le nombre d'or,

Une impressionnante formule dûe à Ramanujan...

... qu'il a découverte en 1910 et dont il n'a donné aucune démonstration. Cette formule est diablement efficace puisqu'elle fournit 8 décimales à chaque itération. Elle fut démontrée en 1985 par les frères Borwein (Jonathan et Peter).

Pi en probabilités et statistiques

	Aire de la courbe de Gauss (Espérance mathématique de la loi normale) Démonstration : à télécharger au format Word
	L'aiguille de Buffon : probabilité pour qu'une aiguille de longueur 1 cm, lancée (au hasard) sur un parquet dont les lames sont larges de 2 cm coupe le bord d'une lame.
	L'aiguille de Buffon (généralisée) : probabilité pour qu'une aiguille de longueur 2a cm, lancée (au hasard) sur un parquet dont les lames sont larges de 2b cm coupe le bord d'une lame.
	probabilité pour qu'une fléchette lancée (au hasard) sur une cible carré se plante à l'intérieur du cercle inscrit dans le carré (méthode de Monte Carlo)
	probabilité de tirer exactement n piles et n faces parmi 2n lancers de pièces
	probabilité pour que deux nombres entiers pris au hasard soient premiers entre eux Césaro (1859-1906),formule démontrée en 1881.
p	Rapport entre la longueur réelle d'un fleuve et la distance à vol d'oiseau entre la source et l'embouchure du fleuve...

Liens entre n ! et Pi : la fonction Gamma
Soit la fonction Gamma défine par

G coïncide avec n! pour x entier :
On a aussi : ; ;

Puisque la dérivée de Arctan x est 1/(1+x²) :

Et beaucoup d'autres :

Formules et algorithmes pour évaluer pi
Beaucoup de formules, des notes historiques et des démonstrations. Un excellent travail !
Auteur : Gérard Sookahet
Fichier pdf zippé (60 pages) : 344ko
Dans le merveilleux livre Le Fascinant nombre Pi de Jean-Paul Delahaye qui m'a donné envie de construire ce site.
Renseignement sur ce livre : http://www.pour-la-science.com
Sur le site de Boris Gourevitch.

Retour vers le haut de la page

Un poème pour retenir p
Ces poèmes sont des moyens mnémotechniques pour retenir quelques décimales dans diverses langues en comptant le nombre de lettre de chaque mot.
La longueur de chaque mot donne une décimale (un mot de 10 lettres code zéro). La ponctuation ne code rien.

En français

Que j'aime à faire apprendre ce nombre utile aux sages !	3 1 4 1 5 9 2 6 5 3 5
Immortel Archimède, artiste ingénieur,	8 9 7 9
Qui de ton jugement peut priser la valeur ?	3 2 3 8 4 6 2 6
Pour moi, ton problème eut de pareils avantages.	4 3 3 8 3 2 7 9
Jadis, mystérieux, un problème bloquait	5 0 2 8 8
Tout l'admirable procédé, l'œuvre grandiose	4 1 9 7 1 6 9
Que Pythagore découvrit aux anciens Grecs.	3 9 9 3 7 5
0 quadrature ! Vieux tourment du philosophe	1 0 5 8 2 9
Insoluble rondeur, trop longtemps vous avez	9 7 4 9 4 4
Défié Pythagore et ses imitateurs.	5 9 2 3 0
Comment intégrer l'espace plan circulaire ?	7 8 1 6 4 0
Former un triangle auquel il équivaudra ?	6 2 8 6 2 0
Nouvelle invention : Archimède inscrira	8 9 9 8
Dedans un hexagone ; appréciera son aire	6 2 8 0 3 4
Fonction du rayon. Pas trop ne s'y tiendra :	8 2 5 3 4 2 1 1 7
Dédoublera chaque élément antérieur ;	0 6 7 9
Toujours de l'orbe calculée approchera ;	8 2 1 4 8 0
Définira limite ; enfin, l'arc, le limiteur	8 6 5 1 3 2 8
De cet inquiétant cercle, ennemi trop rebelle	2 3 0 6 6 4 7
Professeur, enseignez son problème avec zèle	0 9 3 8 4 4

Une variante de ce poème (sur le début)
Que j'aime à faire apprendre un nombre utile aux sages !
Glorieux Archimède, artiste, ingénieur,
Toi de qui Syracuse aime encore la gloire,
Soit ton nom conservé par de savants grimoires !
Le reste est identique au précédent

Un autre plus court
Car j'aime à faire apprécier ce nombre, objet des soins patients, longtemps répétés, engendrés par ce dur problème grec : "carrer" le cercle. Même son nom habituel est un symbole (périmètre) utile.

En anglais

Yes, I have a great statement to relate.
May I have a large container of coffee
How I wish I could recollect of circle round
The exact relation Archimede unwound.
How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!
How I wish I could enumerate Pi easily, since all these horrible mnemonics prevent recalling any of pi's sequence more simply.
See, I have a rhyme assisting my feeble brain,
its tasks sometimes resisting.
But a time I spent wandering in bloomy night ;
Yon tower, tinkling chimewise, loftily opportune.
Out, up, and together came sudden to Sunday rite,
The one solemnly off to correct plenilune.

Un poème d'Edgar Poe
Near a Raven
Midnights so dreary, tired and weary.
Silently pondering volumes extolling all by-now obsolete lore.
During my rather long nap - the weirdest tap!
An ominous vibrating sound disturbing my chamber's antedoor.
"This", I whispered quietly, "I ignore"…

Cliquez pour lire le poème en entier

En allemand

Dir, o Held, o Alter Philosoph, du Reisen-Genie !
Wie, viele Tausende bewundern Geister
Himmlisch wie du und Göttlich !
Noch reiner in Aeonen
Wird das uns strahlen ,
Wie im lichten Morgenrot !
Wie ? O ! Dies p
Macht ernstlich so vielen viele Müh !
Lernt immerhin, Jünglinge, leichte Verselein,
Wie so zum Beispiel dies dürfte zu merken sein !

En espagnol

Con 1 palo y 5 ladrillos se pueden hacer mil cosas.
Sol y Luna y cielo proclaman al divino autor del cosmo.

En portugais

Sim, é'util e fácil memorizar um n'ugrato aos sábios.
Sou o medo e temor constante do menino vadio.

En danois

Eva, o lief, o zoete hartedief uw blauwe oogen zyn wreed bedrogen.

En albanais

Kur e shoh e mesoj sigurisht.

En breton

Piv a zebr a-walc'h dimerc'her ?
Ne lavaro netra, tud Breizh !

Retour vers le haut de la page

Des programmes de calcul de p en javascript

Calcul de p par l'algorithme compte-goutte

Calcul de p par une méthode statistique

Calcul de p par la formule d' arctan( 1 )

Calcul de p avec la formule de Machin

Calcul de p avec la méthode des polygones

Calcul de p par l'algorithme de Pif

Retour vers le haut de la page

Calcul de p par par l'algorithme compte-goutte

Cet algorithme est le plus efficace de tous les algorithmes proposés ici.
Le script est la retranscription en javascript du programme que je propose en quickbasic au paragraphe Des décimales du nombre p qui calcule 2400 décimales.

A noter : javascript n'est pas un très bon langage de calcul et rame un peu si vous lui en demandez trop avec cet algorithme...

Lancer le calcul par cette méthode

Retour au menu des calculs de p

Calcul de p par une méthode statistique

Le rapport entre l'aire du quart de disque et l'aire du carré est de p/4
On choisit au hasard des points dans le carré et on compte ceux qui sont dans le quart de disque.

On a alors : p = 4 x (nb de points dans le quart de disque) / (nb de points dans le carré)

Lancer le calcul par cette méthode
(La fenêtre peut être longue à s'ouvrir. Pas de panique, c'est le processeur qui travaille dur !)

Remarque : Cette méthode de calcul peut-être appliquée à la maison avec un jeu de fléchette, par exemple, et beaucoup, beaucoup de patience...

Retour au menu des calculs de p

Calcul de p par la formule d' arctan( 1 )
On utilise la formule :

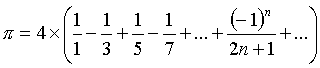
Cette formule vient de :	pour \|x\| <=1
et en particulier de	Arctan( 1 ) =

Lancer le calcul par cette méthode

Retour au menu des calculs de p

Calcul de p avec la formule de Machin
On utilise la formule de Machin :

et le développement de Arctan x en série entière :

Lancer le calcul par cette méthode

Retour au menu des calculs de p

Calcul de p par la méthode des polygones inscrits
La méthode consiste à calculer le périmètre du polygone régulier à 2ⁿ côtés inscrit dans le cercle de rayon 1.
Ce périmètre tend vers 2p

Lancer le calcul par cette méthode

Retour au menu des calculs de p

Un peu moins sérieux : calcul d'une décimale isolée de p par l'algorithme de Pif
Il est très rapide, très simple à programmer et très rapide. En voici une implémentation en javascript :

Entrez le rang de la décimale de pi cherchée et appuyez sur le bouton.
Remarque : dans "3,14" , 3 est la décimale de rang 0 , 1 est la décimale de rang 1, 4 est la décimale de rang 2, etc ...

Retour au menu des calculs de p

Retour vers le haut de la page

Des petites choses marrantes

Une charade...
Mon premier est un animal qui travaille avec sa queue et qui n'a rien pour s'asseoir...
Mon deuxième est un animal qui travaille avec sa queue et qui n'a rien pour s'asseoir...
Mon troisième est un animal qui travaille avec sa queue et qui n'a rien pour s'asseoir...
Mon tout est un nombre bien connu de tout le monde

Pour avoir la réponse, positionnez la souris sur l'image suivante et attendez

Une fraction surprenante...

= p

Démonstration ...

Et d'autres !
1) La hauteur d'un éléphant (des pieds aux épaules) est 2*Pi*D où D est le diamètre de ses pieds.
2) 3,14 est le rapport entre la longueur d'un fleuve et sa longueur à vol d'oiseau.
3) Prenez 1000 couples mariés, mesurez pour chacun la taille h de l'homme et f de la femme en mm, comptez le nombre N de fois que h et f sont premiers entre-eux, alors la racine carrée de 6000/N est une valeur approchée de Pi.

Retour vers le haut de la page

Calculer pi avec des élèves
Il est possible de faire calculer pi par des élèves de collège. Je vous propose trois activités destinées à différents niveaux (testées en classe)

Activité niveau 6ème : en mesurant des périmètres
Activité niveau 5ème : en mesurant une aire
Activité niveau 4ème / 3ème : par des calculs sur les fractions (sommes partielles d'une série ou fractions réduites du développement de pi en fraction continue)

Cliquez ici pour voir ces activités en détails.

Une autre activité possible consiste à démontrer le développement en série entière de arctan x et de calculer arctan (1).
(Euh ... Activité encore non-testée actuellement !)

Retour vers le haut de la page

Quelques liens vers des sites sur p

	www.pi314.net (Le monde de pi ) : LE site français sur pi par Boris Gourevitch ! Un boulot impressionnant, un gars passionné et très sympa.
	www.peripheria.net : le site "portail" sur pi, par Miha. Très belle présentation.
	www.nombrepi.com : un très beau site sur pi.

L'antre de miha : l'ancienne version du site de Miha.
A propos de pi
Dossiers du Rallye 1999 : sur pi et le nombre d'or

Am I in Pi : trouver sa date de naissance dans les décimales de pi. INCONTOURNABLE !
The Pi Pages
The constant pi

http://www.pour-la-science.com : ce n'est pas un site sur pi mais vous pourrez y commander le merveilleux livre de Jean-Paul Delahaye Le Fascinant nombre Pi qui m'a donné envie de construire ce site.

Retour vers le haut de la page

Rang de la décimale cherchée :
Décimale cherchée :